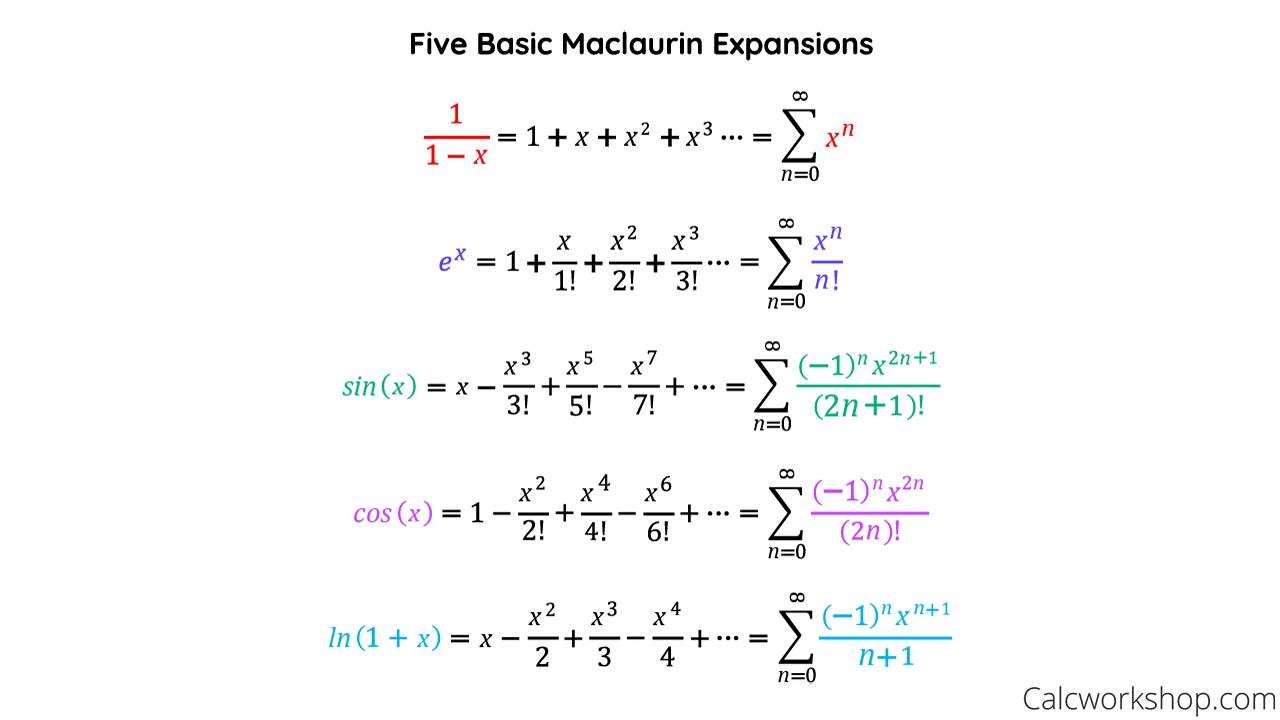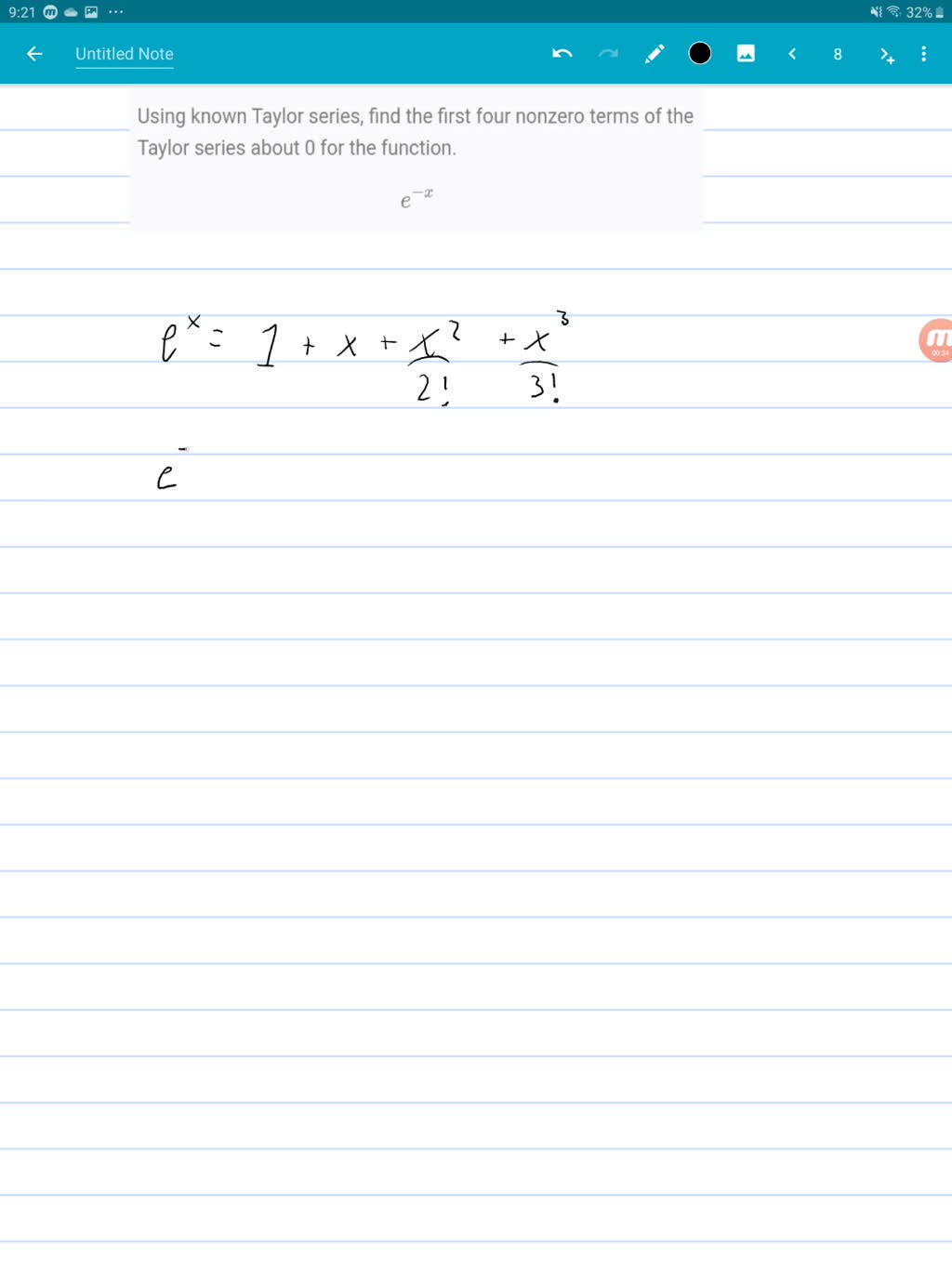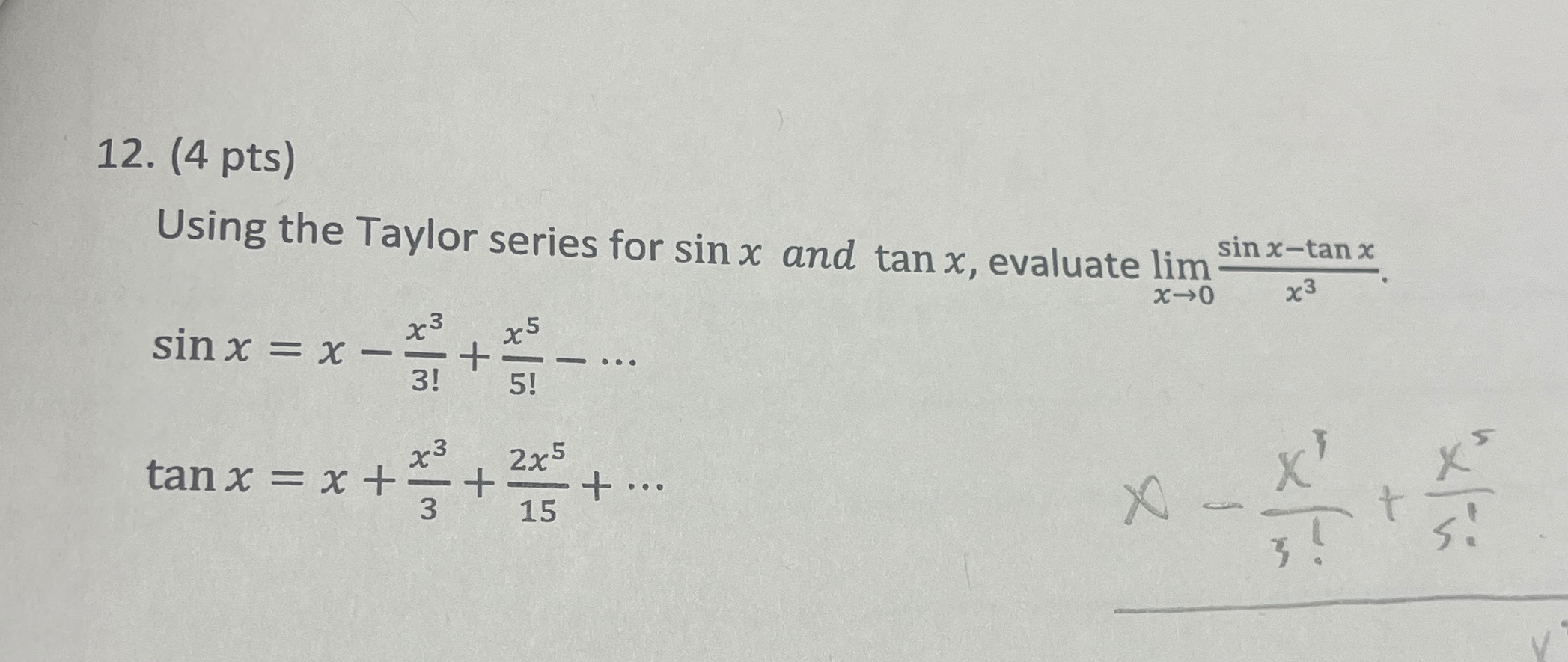Tanx Taylor Series - So you finally can write your taylor series as: Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by. The radius of convergence of the power series expansion of $\tan x$ around. The tangent function has a taylor series expansion: \(\ds \tan x\) \(\ds \sum_{n. (as one might guess, the series for $\tanh$ is the same, with the sign correction. Tan(x) = x + 1 3x3 + 2 15x5 + o(x7) which is.
So you finally can write your taylor series as: The tangent function has a taylor series expansion: Tan(x) = x + 1 3x3 + 2 15x5 + o(x7) which is. The radius of convergence of the power series expansion of $\tan x$ around. (as one might guess, the series for $\tanh$ is the same, with the sign correction. \(\ds \tan x\) \(\ds \sum_{n. Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by.
The tangent function has a taylor series expansion: Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by. The radius of convergence of the power series expansion of $\tan x$ around. Tan(x) = x + 1 3x3 + 2 15x5 + o(x7) which is. (as one might guess, the series for $\tanh$ is the same, with the sign correction. So you finally can write your taylor series as: \(\ds \tan x\) \(\ds \sum_{n.
Solved The Taylor series expansion of the tanx function is
The tangent function has a taylor series expansion: Tan(x) = x + 1 3x3 + 2 15x5 + o(x7) which is. (as one might guess, the series for $\tanh$ is the same, with the sign correction. So you finally can write your taylor series as: Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by.
Taylor Series
So you finally can write your taylor series as: The radius of convergence of the power series expansion of $\tan x$ around. The tangent function has a taylor series expansion: (as one might guess, the series for $\tanh$ is the same, with the sign correction. Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by.
Solved QUESTION 5 The Taylor series of y = tanx about x =
So you finally can write your taylor series as: (as one might guess, the series for $\tanh$ is the same, with the sign correction. Tan(x) = x + 1 3x3 + 2 15x5 + o(x7) which is. Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by. The radius of convergence of the power series expansion of $\tan x$.
SOLVED The Taylor series expansion of the tanx function is as follows
\(\ds \tan x\) \(\ds \sum_{n. The tangent function has a taylor series expansion: Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by. (as one might guess, the series for $\tanh$ is the same, with the sign correction. The radius of convergence of the power series expansion of $\tan x$ around.
SOLVED 8.Find the first three terms Of the Taylor Series for f
So you finally can write your taylor series as: The tangent function has a taylor series expansion: (as one might guess, the series for $\tanh$ is the same, with the sign correction. Tan(x) = x + 1 3x3 + 2 15x5 + o(x7) which is. Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by.
Math Marvels Why 215 Maclaurin Series Expansion Of Tanx
The tangent function has a taylor series expansion: Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by. (as one might guess, the series for $\tanh$ is the same, with the sign correction. So you finally can write your taylor series as: Tan(x) = x + 1 3x3 + 2 15x5 + o(x7) which is.
Math Marvels Why 215 Maclaurin Series Expansion Of Tanx
\(\ds \tan x\) \(\ds \sum_{n. The radius of convergence of the power series expansion of $\tan x$ around. So you finally can write your taylor series as: (as one might guess, the series for $\tanh$ is the same, with the sign correction. Tan(x) = x + 1 3x3 + 2 15x5 + o(x7) which is.
Solved (4 pts)Using the Taylor series for sinx and tanx,
The tangent function has a taylor series expansion: Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by. (as one might guess, the series for $\tanh$ is the same, with the sign correction. The radius of convergence of the power series expansion of $\tan x$ around. \(\ds \tan x\) \(\ds \sum_{n.
Solved Taylor series expansion of the tanx function is as
(as one might guess, the series for $\tanh$ is the same, with the sign correction. So you finally can write your taylor series as: Tan(x) = x + 1 3x3 + 2 15x5 + o(x7) which is. \(\ds \tan x\) \(\ds \sum_{n. The radius of convergence of the power series expansion of $\tan x$ around.
Solved QUESTION 5 The Taylor series of y = tanx about x =
\(\ds \tan x\) \(\ds \sum_{n. Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by. (as one might guess, the series for $\tanh$ is the same, with the sign correction. The tangent function has a taylor series expansion: So you finally can write your taylor series as:
Tan(X) = X + 1 3X3 + 2 15X5 + O(X7) Which Is.
The tangent function has a taylor series expansion: Compute answers using wolfram's breakthrough technology & knowledgebase, relied on by. So you finally can write your taylor series as: The radius of convergence of the power series expansion of $\tan x$ around.
\(\Ds \Tan X\) \(\Ds \Sum_{N.
(as one might guess, the series for $\tanh$ is the same, with the sign correction.