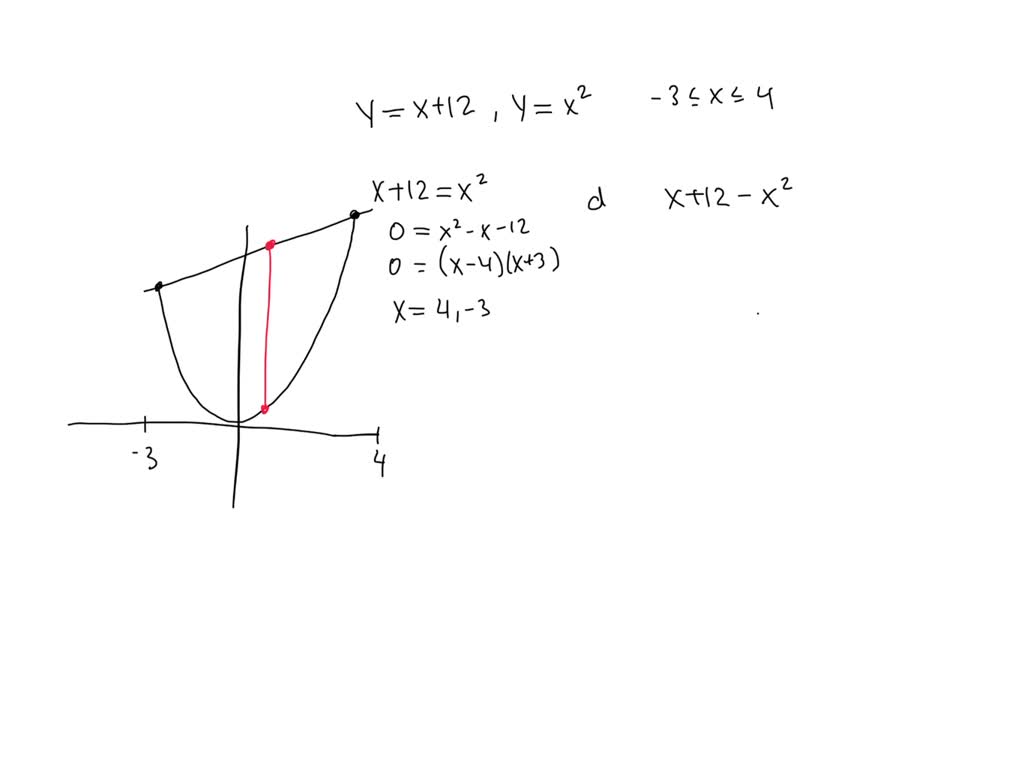
What Is The Maximum Vertical Distance Between The Line - The maximum distance is 4289 and can be found at x = 21. What is the maximum vertical distance between the line y = x + 20 and the. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. Find the value of x x which maximizes this using the. The distance=|x2 − x − 30| | x 2 − x − 30 |. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1.
What is the maximum vertical distance between the line y = x + 20 and the. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. The maximum distance is 4289 and can be found at x = 21. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. Find the value of x x which maximizes this using the. The distance=|x2 − x − 30| | x 2 − x − 30 |.
The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. The distance=|x2 − x − 30| | x 2 − x − 30 |. Find the value of x x which maximizes this using the. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. What is the maximum vertical distance between the line y = x + 20 and the. The maximum distance is 4289 and can be found at x = 21.
Solved Determine the maximum vertical distance between the
The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. What is the maximum vertical distance between the line y = x +.
SOLVED What is the maximum vertical distance between the line y = x
The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. Find the value of x x which maximizes this using the. The distance=|x2 − x − 30| | x 2 − x − 30 |. The maximum distance is.
What is the Maximum Vertical Distance Between Y=X+2 and Y=X^2
The distance=|x2 − x − 30| | x 2 − x − 30 |. Find the value of x x which maximizes this using the. The maximum distance is 4289 and can be found at x = 21. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola.
Solved What is the maximum vertical distance between the line y=x+2
The distance=|x2 − x − 30| | x 2 − x − 30 |. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) =.
What is the maximum vertical distance between the line y=x+ Quizlet
The maximum distance is 4289 and can be found at x = 21. Find the value of x x which maximizes this using the. What is the maximum vertical distance between the line y = x + 20 and the. To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy. The distance=|x2 − x.
Solved What is the maximum vertical distance between the line y=x+30
Find the value of x x which maximizes this using the. What is the maximum vertical distance between the line y = x + 20 and the. The maximum distance is 4289 and can be found at x = 21. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of.
[Solved] What is the maximum vertical distance between the line y = x
The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. The maximum distance is 4289 and can be found at x = 21. Find the value of x x which maximizes this using the. What is the maximum vertical.
SOLVED Optimization What is the maximum vertical distance between
The distance=|x2 − x − 30| | x 2 − x − 30 |. The maximum distance is 4289 and can be found at x = 21. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. Find the value of x x which maximizes this using.
SOLVEDWhat is the maximum vertical distance between the line y=x+2 and
What is the maximum vertical distance between the line y = x + 20 and the. The distance=|x2 − x − 30| | x 2 − x − 30 |. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. The derivative of g(x) g (x), g′(x).
What is the Maximum Vertical Distance Between Y=X+2 and Y=X^2
The distance=|x2 − x − 30| | x 2 − x − 30 |. Find the value of x x which maximizes this using the. The derivative of g(x) g (x), g′(x) = 2x g ′ (x) = 2 x is inferior to that of f(x) f (x), f′(x) = 1 f ′ (x) = 1. What is the maximum.
The Derivative Of G(X) G (X), G′(X) = 2X G ′ (X) = 2 X Is Inferior To That Of F(X) F (X), F′(X) = 1 F ′ (X) = 1.
The maximum distance is 4289 and can be found at x = 21. Find the value of x x which maximizes this using the. What is the maximum vertical distance between the line y = x + 20 y = x + 20 and the parabola y. What is the maximum vertical distance between the line y = x + 20 and the.
The Distance=|X2 − X − 30| | X 2 − X − 30 |.
To find the maximum vertical distance, we need to find the maximum value of $$\delta y$$δy.